Multithreading#

What are threads?#

Threads are execution units within a process that can run simultaneously.

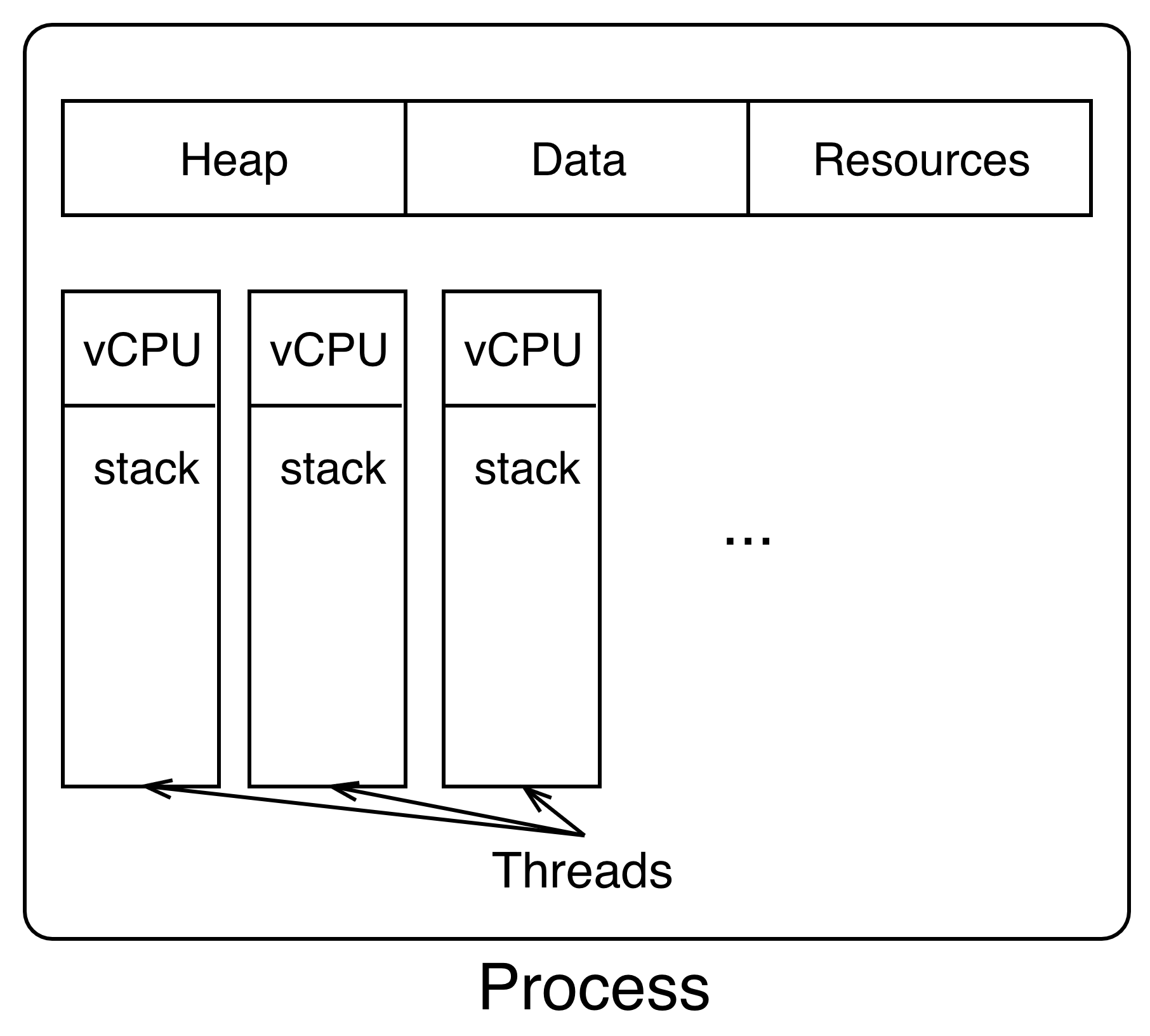
While processes are entirely separate, threads run in a shared memory space.

Starting Julia with multiple threads#

By default, Julia starts with a single user thread. We must tell it explicitly to start multiple user threads. There are two ways to do this:

Environment variable: JULIA_NUM_THREADS=4
Command line argument: julia -t 4 or, equivalently, julia --threads 4

Jupyter lab:

The simplest way is to globally set the environment variable JULIA_NUM_THREADS (e.g. in the .bashrc). But one can also create a specific Jupyter kernel for multithreaded Julia:

using IJulia
installkernel("Julia (4 threads)", env=Dict("JULIA_NUM_THREADS"=>"4"))

We can readily check how many threads we are running:

Threads.nthreads()

User threads vs default threads#

Technically, the Julia process is also spawning multiple threads already in “single-threaded” mode, like

a thread for unix signal listening
multiple OpenBLAS threads for BLAS/LAPACK operations

For this reason, we call the threads specified via --threads or the environment variable user threads or simply Julia threads.

Task-based multithreading#

Conceptually, Julia implements task-based multithreading. In this paradigm, a task - e.g. a computational piece of a code - is marked for parallel execution on any of the available Julia threads. Julias dynamic scheduler will automatically put the task on one of the threads and trigger the execution of the task on said thread.

Ideally, a user should think about tasks and not threads.

Advantages:

high-level and convenient
composability / nestability (Multithreaded code can call multithreaded code can call multithreaded code ….)

Disadvantages:

scheduling overhead
can get in the way when performance engineering
- scheduler has limited information (e.g. about the system topology)
- low-level profiling (e.g. with LIKWID) currently requires a known task -> thread -> cpu core mapping.

(Blog post: Announcing composable multi-threaded parallelism in Julia)

Spawning tasks on threads: `Threads.@spawn`#

Threads.@spawn spawns a task on a Julia thread. Specifically, it creates (and immediately returns) a Task and schedules it for execution on an available Julia thread.

Note the conceptual similarity between Threads.@spawn (task -> thread) and Distributed.@spawn (task -> process) and also @async.

To avoid having to prefix Threads. to @spawn (and other threading-related functions) let’s load everything from Base.Threads into global scope.

using Base.Threads

@spawn println("test")

Task (runnable) @0x00007fc137014e70

test

While Threads.@spawn returns the task right away - it is non-blocking - the result might only be fetchable after some time.

t = @spawn begin
    sleep(3)
    "result"
end
@time fetch(t)

  2.966058 seconds (1.97 k allocations: 92.584 KiB, 0.14% compilation time)

"result"

Note that we can use (some of) the control flow tools that we’ve already covered, like @sync.

@sync t = @spawn begin
    sleep(3)
    "result"
end
@time fetch(t)

  0.000004 seconds

"result"

for i in 1:2*nthreads()
    @spawn println("Hi, I'm ", threadid())
end

Hi, I'm

Example: Recursive Fibonacci series#

\[ F(n) = F(n-1) + F(n-2), \qquad F(1) = F(2) = 1\]

We can nest @spawn calls freely!

function fib(n)
    n < 2 && return n
    t = @spawn fib(n - 2)
    return fib(n - 1) + fetch(t)
end

fib (generic function with 1 method)

Hi, I'm

fib.(1:10)

Hi, I'm 4
Hi, I'm 4
Hi, I'm 4
Hi, I'm 4
Hi, I'm 3
Hi, I'm 2

10-element Vector{Int64}:
  1
  1
  2
  3
  5
  8
 13
 21
 34
 55

(Note: Algorithmically, this is a highly inefficient implementation of the Fibonacci series, of course!)

Example: `tmap` (like `pmap`)#

tmap(fn, itr) = map(fetch, map(i -> Threads.@spawn(fn(i)), itr))

tmap (generic function with 1 method)

using LinearAlgebra

M = [rand(200, 200) for i in 1:10];

tmap(svdvals, M)

10-element Vector{Vector{Float64}}:
 [100.67123284487788, 7.950696623567239, 7.811301993806787, 7.748513398259706, 7.647340773555297, 7.486770200118421, 7.434659449253653, 7.3489803649959935, 7.302700658576302, 7.177473045356274  …  0.3342916425720595, 0.29013326787177235, 0.25233485084735274, 0.23471255912630906, 0.19093098367303216, 0.1455552981008333, 0.14296203356464485, 0.09800166652318565, 0.03184772428525276, 0.005265312445710739]
 [100.38425255546677, 7.950407654067494, 7.775177144306881, 7.733360600067993, 7.578645245357895, 7.498041743416242, 7.47984650237933, 7.437711431317731, 7.350562344919744, 7.307576509924039  …  0.3091656604537736, 0.2737800626073915, 0.2512987408346807, 0.22046902858533338, 0.1684177679072846, 0.14050144269228215, 0.12257329102795181, 0.06618114130384002, 0.061878925395953494, 0.004725864093933092]
 [100.12180100531361, 8.062188047628604, 7.95809279060523, 7.771366284363079, 7.658421622261246, 7.495886647214599, 7.452412108318767, 7.4178999468994995, 7.339244283862941, 7.311665671542621  …  0.31368378176578454, 0.2639902415745525, 0.22910880208715306, 0.19014860491260752, 0.16241274005904432, 0.14270546300869374, 0.11686555487489741, 0.10581841997530474, 0.05753975562503835, 0.045582383395510774]
 [100.20453278162591, 8.013280164102268, 7.896522369733462, 7.773784440824388, 7.716175198579731, 7.641462853662889, 7.527708601136462, 7.494072099019246, 7.366032096191476, 7.256728999388528  …  0.2610963371773936, 0.23246617095574032, 0.20210064783955595, 0.1713868907387135, 0.15177386548433033, 0.14024865928146454, 0.10644640576172186, 0.0769826734794836, 0.07082631862054117, 0.05591652735370335]
 [99.92277844337461, 8.004762343679577, 7.868944514125499, 7.813428354648061, 7.605930548982613, 7.576145460734679, 7.515439169292759, 7.447361459239769, 7.349939424363516, 7.228427800556619  …  0.28858715126279577, 0.2504249693710346, 0.22342760119336505, 0.18655237879226377, 0.1809542240563175, 0.13266083328018008, 0.11036850909024944, 0.07374425216620147, 0.0381897628560015, 0.003548842523270397]
 [100.20260966406543, 8.0256913997432, 7.793138426941864, 7.7181543297209805, 7.624057624486687, 7.533462887954394, 7.51402389251016, 7.421186247086893, 7.248597734179209, 7.238319373521701  …  0.25734574514127595, 0.22779751833253672, 0.20324840410939699, 0.16336042769352355, 0.1489157788164038, 0.13484107785720642, 0.10161930626045795, 0.07904893750280294, 0.03505794337753627, 0.001779377881281236]
 [99.90365179690002, 7.939230313766951, 7.856781834777159, 7.785585209447371, 7.608946526020202, 7.497846408320733, 7.435228962474984, 7.353157907136937, 7.334766776944602, 7.264332426175999  …  0.35536116598686585, 0.32229916886100857, 0.2905639493264572, 0.2358067885872965, 0.18927585965355986, 0.10403945941139421, 0.0899638630413736, 0.075851057193002, 0.026095765679992923, 0.007966347151493086]
 [100.18462238499495, 8.129606979584947, 7.945182468387494, 7.82068179006931, 7.780727151645908, 7.690115351210205, 7.647414865653439, 7.404157947073155, 7.365360574271029, 7.269629355011812  …  0.3155433301427828, 0.2941993995626135, 0.28659926865954866, 0.2576691194865118, 0.22003888380104553, 0.1406382947139471, 0.10700762414974818, 0.07670427514541671, 0.019500327382097442, 0.001372859898893531]
 [100.59461304340726, 8.043718323597545, 7.800906387951628, 7.75332315343476, 7.54636567244683, 7.510426809191562, 7.479613271534397, 7.343203729415979, 7.288526735127726, 7.250036202666924  …  0.27850723679292355, 0.2639234346969243, 0.2393304418547091, 0.22333469290654645, 0.16981178894027552, 0.15323252507574153, 0.10311066352957252, 0.08013241474638218, 0.05371007769920253, 0.005404485963796817]
 [100.14901805054043, 7.981394660068511, 7.81983973909683, 7.776557643287288, 7.680316003288309, 7.483671424604455, 7.410924968805952, 7.364236654652344, 7.349123171358512, 7.250465041994171  …  0.2904217270496274, 0.26115607411237113, 0.2329456257205222, 0.18953501679905932, 0.15567448524477973, 0.14655999068451767, 0.07110421624317681, 0.05123824209421516, 0.022095836580959604, 0.005723017061350942]

tmap(i -> println(i, " ($(threadid()))"), 1:10);

(1)
(1)
(1)
(1)
(1)
(1)
(1)
(2)
(4)
(3)

Note, however, that this implementation creates temporary allocations and thus isn’t particularly efficient.

using BenchmarkTools

@btime tmap($svdvals, $M);
@btime map($svdvals, $M);

  28.870 ms (145 allocations: 4.22 MiB)

  62.910 ms (81 allocations: 4.22 MiB)

Remarks on `@spawn`#

Task migration: Not only does the scheduler dynamically assign tasks to Julia threads, but it is also free to move tasks between threads. Hence, threadid() isn’t necessarily constant over time and should be used with care!
Spawning tasks on specific threads: Julia doesn’t have a built-in tool for this (as of now). However, some packages like ThreadPinning.jl export @tspawnat <threadid> ... which allows to spawn sticky tasks.

using ThreadPinning

@tspawnat 3 println("running on thread ", threadid())

Task (runnable) @0x00007fc137014b90

Multithreading for-loops: `@threads`#

Higher level interface to multithreading. (Compare Distributed.@spawnat vs @distributed)

@threads for i in 1:2*nthreads()
    println("Hi, I'm ", threadid())
end

running on thread 3
Hi, I'm 2
Hi, I'm 1
Hi, I'm 2
Hi, I'm 4
Hi, I'm 4
Hi, I'm 3
Hi, I'm 3
Hi, I'm 4

using BenchmarkTools

function square!(x)
    for i in eachindex(x)
        x[i] = x[i]^2
    end
end

function square_threads!(x)
    @threads for i in eachindex(x)
        x[i] = x[i]^2
    end
end

x = rand(1_000_000)
@btime square!($x);
@btime square_threads!($x);

  327.594 μs (0 allocations: 0 bytes)

  86.436 μs (24 allocations: 2.05 KiB)

Scheduling options#

Syntax: @threads [schedule] for ...

:dynamic (default)
- creates O(nthreads()) many tasks each processing a contigious region of the iteration space
- each task essentially spawned with @spawn
  - -> task migration
  - -> composability / nestability
:static
- evenly splits up the iteration space and creates one task per block
- statically maps tasks to threads, specifically: task 1 -> thread 1, task 2 -> thread 2, etc.
  - -> no task migration, i.e. fixed task-thread mapping
  - -> not composable / nestable
  - -> only little overhead

@threads :dynamic for i in 1:2*nthreads()
    println(i, " -> thread ", threadid())
end

-> thread 3
-> thread 3
-> thread 2
-> thread 2
-> thread 1
-> thread 3
-> thread 4
-> thread 4

@threads :static for i in 1:2*nthreads()
    println(i, " -> thread ", threadid())
end

-> thread 3
-> thread 4
-> thread 1
-> thread 4
-> thread 1
-> thread 3
-> thread 2
-> thread 2

For @threads :static, every thread handles precisely two iterations!

@threads :dynamic for i in 1:3
    @threads :dynamic for j in 1:3
        println("$i, $j")
    end
end

1, 2
3, 3
2, 1
1, 3
2, 3
3, 2
1, 1
3, 1
2, 2

@threads :static for i in 1:3
    @threads :static for j in 1:3
        println("$i, $j")
    end
end

TaskFailedException

    nested task error: `@threads :static` cannot be used concurrently or nested
    Stacktrace:
     [1] error(s::String)
       @ Base ./error.jl:35
     [2] macro expansion
       @ ./threadingconstructs.jl:91 [inlined]
     [3] macro expansion
       @ ./In[21]:2 [inlined]
     [4] (::var"#161#threadsfor_fun#41"{var"#161#threadsfor_fun#39#42"{UnitRange{Int64}}})(tid::Int64; onethread::Bool)
       @ Main ./threadingconstructs.jl:84
     [5] #161#threadsfor_fun
       @ ./threadingconstructs.jl:51 [inlined]
     [6] (::Base.Threads.var"#1#2"{var"#161#threadsfor_fun#41"{var"#161#threadsfor_fun#39#42"{UnitRange{Int64}}}, Int64})()
       @ Base.Threads ./threadingconstructs.jl:30

Stacktrace:
 [1] wait
   @ ./task.jl:345 [inlined]
 [2] threading_run(fun::var"#161#threadsfor_fun#41"{var"#161#threadsfor_fun#39#42"{UnitRange{Int64}}}, static::Bool)
   @ Base.Threads ./threadingconstructs.jl:38
 [3] top-level scope
   @ ./threadingconstructs.jl:93

Load-balancing#

function compute_nonuniform_spawn!(a, niter=zeros(Int, nthreads()), load=zeros(Int, nthreads()))
    @sync for i in 1:length(a)
        Threads.@spawn begin
            a[i] = sum(abs2, rand() for j in 1:i)

            # only for bookkeeping
            niter[threadid()] += 1
            load[threadid()] += i
        end
    end
    return niter, load
end

compute_nonuniform_spawn! (generic function with 3 methods)

a = zeros(nthreads() * 20)
niter, load = compute_nonuniform_spawn!(a)

([1, 75, 1, 3], [9, 3191, 3, 37])

using Plots

b1 = bar(niter, xlab="threadid", ylab="# iterations", title="Number of iterations", legend=false)
b2 = bar(load, xlab="threadid", ylab="workload", title="Workload", legend=false)

display(b1)
display(b2)

function compute_nonuniform_threads!(a, niter=zeros(Int, nthreads()), load=zeros(Int, nthreads()))
    @threads for i in 1:length(a)
        a[i] = sum(abs2, rand() for j in 1:i)

        # only for bookkeeping
        niter[threadid()] += 1
        load[threadid()] += i
    end
    return niter, load
end

compute_nonuniform_threads! (generic function with 3 methods)

a = zeros(nthreads() * 20)
niter, load = compute_nonuniform_threads!(a)

([20, 20, 20, 20], [1410, 210, 610, 1010])

b1 = bar(niter, xlab="threadid", ylab="# iterations", title="Number of iterations", legend=false)
b2 = bar(load, xlab="threadid", ylab="workload", title="Workload", legend=false)

display(b1)
display(b2)

(There might be a scheduling option for @threads that implements load-balancing in the future.)

Multithreading: Things to be aware of#

Race conditions and thread safety#

function sum_serial(x)
    s = zero(eltype(x))
    for i in eachindex(x)
        @inbounds s += x[i]
    end
    return s
end

sum_serial (generic function with 1 method)

function sum_threads_naive(x)
    s = zero(eltype(x))
    @threads for i in eachindex(x)
        @inbounds s += x[i]
    end
    return s
end

sum_threads_naive (generic function with 1 method)

numbers = rand(nthreads() * 10_000);

@show sum(numbers);
@show sum_serial(numbers);
@show sum_threads_naive(numbers);

sum(numbers) = 20024.67267607263
sum_serial(numbers) = 20024.672676072696
sum_threads_naive(numbers) = 5098.642407573001

Wrong result! Even worse, it’s non-deterministic and different every time! It’s also slow…

@btime sum_serial($numbers);
@btime sum_threads_naive($numbers);

  53.491 μs (0 allocations: 0 bytes)

  1.431 ms (80026 allocations: 1.22 MiB)

Reason: There is a race condition.

Note that race conditions aren’t specific to reductions. More generally, they can appear when multiple threads are modifying a shared “global” state simultaneously.

Not all of Julia and its packages in the ecosystem are thread-safe! In general, it is safer to assume that they’re not unless proven otherwise.

Fix 1: Divide the work#

function sum_threads_subsums(x)
    blocksize = length(x) ÷ nthreads()
    @assert isinteger(blocksize)
    idcs = collect(Iterators.partition(1:length(x), blocksize))

    subsums = zeros(eltype(x), nthreads())
    @threads for tid in 1:nthreads()
        for i in idcs[tid]
            @inbounds subsums[tid] += x[i]
        end
    end
    return sum(subsums)
end

sum_threads_subsums (generic function with 1 method)

@show sum(numbers);
@show sum_serial(numbers);
@show sum_threads_subsums(numbers);

sum(numbers) = 20024.67267607263
sum_serial(numbers) = 20024.672676072696
sum_threads_subsums(numbers) = 20024.672676072627

@btime sum_threads_subsums($numbers);

  16.397 μs (27 allocations: 2.42 KiB)

Speedup and correct result. But not ideal:

cumbersome to do this manually
can have more subtle performance issues like false sharing

Fix 2: Atomics#

See Atomic Operations in the Julia doc for more information. But in generaly one shouldn’t avoid using them as much as possible since they actually limit the parallelism.

Garbage collection#

As of now, Julia’s GC is not parallel and doesn’t work nicely with multithreading.

If it gets triggered, it essentially “stops the world” (all threads) for clearing up memory.

Hence, when using multithreading, it is even more important to avoid heap allocations!

(If you can’t avoid allocations, consider using multiprocessing instead.)

High-level tools for parallel computing#

ThreadsX.jl #

Parallelized Base functions

using ThreadsX

sum(numbers)

20024.67267607263

ThreadsX.sum(numbers)

20024.67267607263

@btime ThreadsX.sum($numbers);

  24.494 μs (264 allocations: 17.92 KiB)

FLoops.jl #

Fast sequential, threaded, and distributed for-loops for Julia

using FLoops

function sum_floops(x)
    @floop for xi in x
        @reduce(s = zero(eltype(x)) + xi)
    end
    return s
end

sum_floops (generic function with 1 method)

@btime sum_floops($numbers);

  16.974 μs (31 allocations: 1.81 KiB)

numbers = rand(nthreads() * 10_000);

sum_floops(numbers) ≈ sum(numbers)

true

@btime sum_serial($numbers);
@btime sum_floops($numbers);

  53.486 μs (0 allocations: 0 bytes)

  17.129 μs (31 allocations: 1.81 KiB)

@floop supports different executors that allow for easy switching between serial and threaded execution

function sum_floops(x, executor)
    @floop executor for xi in x
        @reduce(s += xi)
    end
    return s
end

sum_floops (generic function with 2 methods)

@btime sum_floops($numbers, $(SequentialEx()));
@btime sum_floops($numbers, $(ThreadedEx()));

  53.486 μs (0 allocations: 0 bytes)

  17.143 μs (29 allocations: 1.80 KiB)

There are many more executors, like DistributedEx or CUDAEx. See, e.g., FoldsThreads.jl and FoldsCUDA.jl.

Under the hood, FLoops is built on top of Transducers.jl (i.e. it translates for-loop semantics into folds).

Tullio.jl #

Tullio is a very flexible einsum macro (Einstein notation)

using Tullio

A = rand(10, 10)
B = rand(10, 10)

C = @tullio C[i, j] := A[i, k] * B[k, j] # matrix multiplication

C ≈ A * B

true

sum_tullio(xs) = @tullio S := xs[i]

sum_tullio (generic function with 1 method)

@btime sum_tullio($numbers);

  3.889 μs (0 allocations: 0 bytes)

(Uses fastmath and other tricks to be faster here.)

LoopVectorization.jl #

Macro(s) for vectorizing loops.

using LoopVectorization

function sum_turbo(x)
    s = zero(eltype(x))
    @tturbo for i in eachindex(x)
        @inbounds s += x[i]
    end
    return s
end

sum_turbo (generic function with 1 method)

@btime sum_turbo($numbers);

  3.621 μs (0 allocations: 0 bytes)

(Uses all kinds of SIMD tricks to be faster than the others.)

System topology and thread affinity#

Hawk compute node#

Not pinning threads (or pinning them badly) can degrade performance massively!

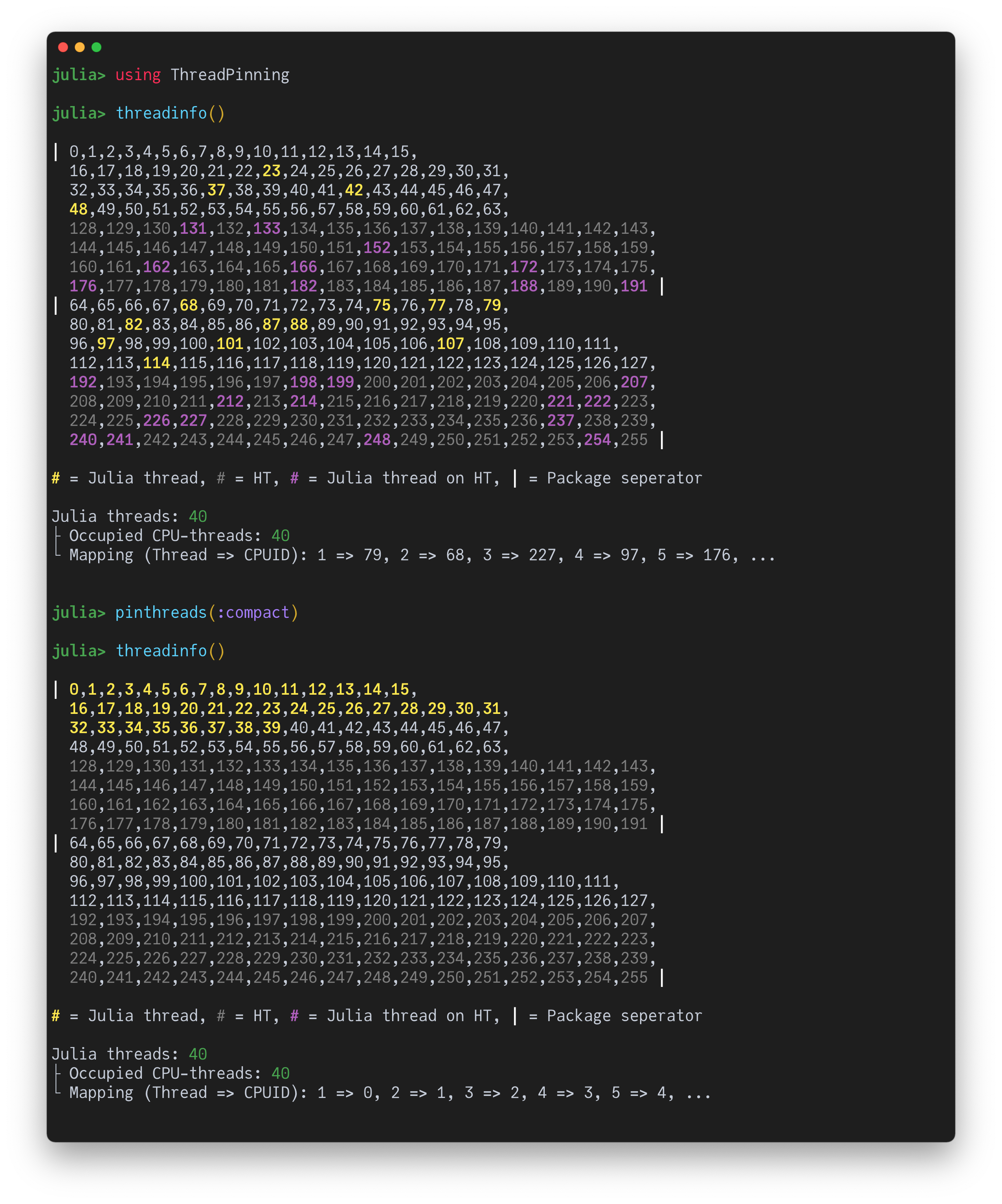
Pinning Julia threads to CPU threads#

What about external tools like numactl, taskset, etc.? Doesn’t work reliably because it can’t distinguish between Julia threads and other internal threads.

Options:

Environment variable: JULIA_EXCLUSIVE=1 (compact pinning)
More control and convenient visualization: ThreadPinning.jl
- compact: pin to cpu thread 0, 1, 2, 3, … one after another
- spread: alternate between sockets so, e.g., 0, 64, 1, 65, 2, 66, …. (if a socket has 64 cores)
- numa: same as spread but alternate between NUMA domains so, e.g., 0, 16, 32, 48, 64, …. (if a NUMA domain has 16 cores)
- Caveat: currently one works on Linux.

Julia for HPC
EuXFEL Workshop

Multithreading

Contents

Multithreading#

What are threads?#

Starting Julia with multiple threads#

User threads vs default threads#

Task-based multithreading#

Spawning tasks on threads: `Threads.@spawn`#

Example: Recursive Fibonacci series#

Example: `tmap` (like `pmap`)#

Remarks on `@spawn`#

Multithreading for-loops: `@threads`#

Scheduling options#

Load-balancing#

Multithreading: Things to be aware of#

Race conditions and thread safety#

Fix 1: Divide the work#

Fix 2: Atomics#

Garbage collection#

High-level tools for parallel computing#

ThreadsX.jl #

FLoops.jl #

Tullio.jl #

LoopVectorization.jl #

System topology and thread affinity#

Hawk compute node#

Pinning Julia threads to CPU threads#

Julia for HPCEuXFEL Workshop

Multithreading

Contents

Multithreading#

What are threads?#

Starting Julia with multiple threads#

User threads vs default threads#

Task-based multithreading#

Spawning tasks on threads: Threads.@spawn#

Example: Recursive Fibonacci series#

Example: tmap (like pmap)#

Remarks on @spawn#

Multithreading for-loops: @threads#

Scheduling options#

Load-balancing#

Multithreading: Things to be aware of#

Race conditions and thread safety#

Fix 1: Divide the work#

Fix 2: Atomics#

Garbage collection#

High-level tools for parallel computing#

ThreadsX.jl#

FLoops.jl#

Tullio.jl#

LoopVectorization.jl#

System topology and thread affinity#

Hawk compute node#

Pinning Julia threads to CPU threads#

Julia for HPC
EuXFEL Workshop

Spawning tasks on threads: `Threads.@spawn`#

Example: `tmap` (like `pmap`)#

Remarks on `@spawn`#

Multithreading for-loops: `@threads`#

ThreadsX.jl #

FLoops.jl #

Tullio.jl #

LoopVectorization.jl #