Optimizing Serial Performance#

At the heart of fast parallel code must be fast serial code. Parallelism can make a good serial code faster. But it can also make a bad code even worse. One can write terribly slow code in any language, including Julia. In this notebook we want to understand what makes Julia code slow and how to detect and avoid common pitfalls. This will lead to multiple concrete performance tips that will help you speed up your Julia code and to write more efficient code in the first place.

By far the most common reasons for slow Julia code are

  • too many (unnecessary) allocations

  • break-down of type inference (e.g. type instabilities)

Avoid Unnecessary Allocations#

Dynamic heap allocations are costly compared to floating point operations. Avoid them, in particular in “hot” loops, because they may trigger garbage collection.

using BenchmarkTools

@btime 1.2 + 3.4;
@btime Vector{Float64}(undef, 1);

  1.694 ns (0 allocations: 0 bytes)

  30.478 ns (1 allocation: 64 bytes)

Example 1: Element-Wise Operations#

function f()
    x = [1, 2, 3]
    for i in 1:10_000
        x = x + 2 * x
    end
    return x
end

f (generic function with 1 method)

@btime f();

  751.011 μs (20001 allocations: 1.53 MiB)

  • Huge number of allocations!

  • Bad sign that they scale with the number of iterations!

Fix 1: Write explicit loops#

function f()
    x = [1, 2, 3]
    for i in 1:100_000
        for k in eachindex(x)
            x[k] = x[k] + 2 * x[k]
        end
    end
    return x
end

@btime f();

  334.203 μs (1 allocation: 80 bytes)

Fix 2: Broadcasting (aka “More Dots”)#

(Recommendation: Old but great blog post by Steven G. Johnson (related notebook))

function f()
    x = [1, 2, 3]
    for i in 1:100_000
        x = x .+ 2 .* x
    end
    return x
end

@btime f();

  3.486 ms (100001 allocations: 7.63 MiB)

function f()
    x = [1, 2, 3]
    for i in 1:100_000
        x .= x .+ 2 .* x
        # or put @. in front
    end
    return x
end

@btime f();

  233.968 μs (1 allocation: 80 bytes)

Fix 3: Immutable Datatypes (if possible)#

using StaticArrays

function f()
  x = @SVector [1, 2, 3]
  for i in 1:100_000
    x = x + 2 * x
  end
  return x
end

@btime f();

  41.822 μs (0 allocations: 0 bytes)

No dynamic heap allocations at all!

Example 2: Linear Algebra#

Spoilers There's a good chance that there will not be a large performance difference between these.

That’s likely because this is an intense enough benchmark that you may begin to run into CPU throttling with a large number of samples, and the slowdown caused by that throttling dominates the average time far more than the improvement of the code.

By lowering the sample size to on the order of dozens (or less) you can see that the first function (on my PC, this will vary) takes roughly 160ms, and the second takes 11ms, an order of magnitude faster.

A slight hint of this may be seen on the benchmark histogram: both have a small clump of results on the far left ast very low times, and the ‘range’ section of the benchmark has a much lower value for the imporved function.

function f()
    A = rand(100, 100)
    B = rand(100, 100)
    s = 0.0
    for i in 1:1_000
        C = A * B
        s += C[i]
    end
    return A
end

a = @benchmark f()

BenchmarkTools.Trial: 65 samples with 1 evaluation.
 Range (min … max):  74.228 ms … 79.241 ms  ┊ GC (min … max): 1.47% … 1.82%
 Time  (median):     77.704 ms              ┊ GC (median):    2.10%
 Time  (mean ± σ):   77.310 ms ±  1.630 ms  ┊ GC (mean ± σ):  1.81% ± 0.51%

              ▁                                      █▃▆▆▁     
  ▇▁▇▁▇▇▁▄▁▄▄▁█▁▄▇▁▁▁▁▄▁▁▁▁▄▄▄▁▁▁▇▄▄▁▁▁▇▇▄▇▄▇▁▁▄▁▁▁▇▄█████▁▄▄ ▁
  74.2 ms         Histogram: frequency by time        79.2 ms <

 Memory estimate: 76.49 MiB, allocs estimate: 2004.

Fix: Preallocate and reuse memory + in-place matrix-multipy#

using LinearAlgebra

function f()
    A = rand(100, 100)
    B = rand(100, 100)
    C = zeros(100, 100) # preallocate
    # C = Array{Float64, 2}(undef, 100, 100)  # A tad faster
    s = 0.0
    for i in 1:100
        mul!(C, A, B) # reuse / in-place matmul
        s += C[i]
    end
    return A
end

b = @benchmark f()

BenchmarkTools.Trial: 720 samples with 1 evaluation.
 Range (min … max):  6.887 ms …  11.159 ms  ┊ GC (min … max): 0.00% … 37.13%
 Time  (median):     6.907 ms               ┊ GC (median):    0.00%
 Time  (mean ± σ):   6.943 ms ± 198.115 μs  ┊ GC (mean ± σ):  0.12% ±  1.51%

      ▃▆█▄                                                     
  ▃▃▅▆██████▄▃▃▃▂▁▁▂▂▁▁▁▂▁▂▂▂▁▁▂▂▃▃▅▇▆▆▆▄▃▃▂▁▂▂▁▁▁▁▂▂▃▃▃▁▂▂▂▂ ▃
  6.89 ms         Histogram: frequency by time        7.04 ms <

 Memory estimate: 234.52 KiB, allocs estimate: 6.

Example 3: Array slicing#

By default, array-slicing creates copies!

using BenchmarkTools

X = rand(3, 3);

f(Y) = Y[:, 1] .+ Y[:, 2] .+ Y[:, 3]

@btime f($X);

  140.366 ns (4 allocations: 320 bytes)

Fix: Views#

f(Y) = @views Y[:, 1] .+ Y[:, 2] .+ Y[:, 3]

# expands to
# f(Y) = view(Y, 1:3, 1) .+ view(Y, 1:3, 2) .+ view(Y, 1:3, 3)

@btime f($X);

  41.772 ns (1 allocation: 80 bytes)

(Note that copying data isn’t always bad)

Example 4: Vectorized Style#

Let’s say we want the sum of the sin of the numbers 1 to 10:

@btime sum(sin.([k for k in 1:10]))  # Dot for broadcast notation
# sum(map(sin, [k for k in 1:10]));  # Equivalent to this

  174.184 ns (2 allocations: 288 bytes)

1.4111883712180104

Fix: Call Directly on Variable#

No need to call sin after the list is generated:

@btime sum([sin(k) for k in 1:10]);

  119.959 ns (1 allocation: 144 bytes)

Fix: Generators and Laziness#

@btime sum(sin(k) for k in 1:10); # generator

  81.264 ns (0 allocations: 0 bytes)

@btime sum(sin, k for k in 1:10); # two-argument version of sum

  81.263 ns (0 allocations: 0 bytes)

How about we do our own sum?

@btime begin
    iter = map(sin, [k for k in 1:10])
    res = 0
    for i in iter
        res += i
    end
end

  173.115 ns (2 allocations: 288 bytes)

@btime begin
    iter = Iterators.map(sin, [k for k in 1:10])  # Lazy map, on an vector
    res = 0
    for i in iter
        res += i
    end
end

  135.819 ns (1 allocation: 144 bytes)

@btime begin
    iter = Iterators.map(sin, k for k in 1:10)  # Lazy map, on a generator
    res = 0
    for i in iter
        res += i
    end
end

  79.274 ns (0 allocations: 0 bytes)

@btime begin
    iter = (sin(k) for k in 1:10)  # Only generator, already lazy
    res = 0
    for i in iter
        res += i
    end
end

  78.917 ns (0 allocations: 0 bytes)

This highlights the point from the first session: user code is as performant as any other code

Try doing this in Numpy and it’s always orders of magnitude slower than the Julia version, with the user-implemented sum being twice as slow as the built-in Numpy sum.

Avoid Type Instabilities#

Type stability: A function f is type stable if for a given set of input argument types the return type is always the same.

In particular, it means that the type of the output of f cannot vary depending on the values of the inputs.

Type instability: The return type of a function f is not predictable just from the type of the input arguments alone.

Instructive example: f(x) = rand() > 0.5 ? 1.23 : "string"

Example: Global scope#

A typical cause of type instability are global variables.

From a compiler perspective, variables defined in global scope can change their value and even their type(!) any time.

a = 2.0
b = 3.0

f() = 2 * a + b

f (generic function with 2 methods)

f()

7.0

@code_warntype f()

MethodInstance for f

()
  from f() in Main at In[22]:4
Arguments
  #self#::Core.Const(f)
Body::Any
1 ─

 %1 = (

2 * Main.a)

::Any
│   %2 = (%1 + Main.b)::Any
└──      return %2

@code_llvm f()

;  @ In[22]:4 within `f`
define 

nonnull {}* @julia_f_2890() #0 {
top:
  %0 = alloca [2 x {}*], align 8
  %gcframe2 = alloca [4 x {}*], align 16
  %gcframe2.sub = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 0
  %.sub = getelementptr inbounds [2 x {}*], [2 x {}*]* %0, i64 0, i64 0
  %1 = bitcast [4 x {}*]* %gcframe2 to i8*
  call void @llvm.memset.p0i8.i32(i8* noundef nonnull align 16 dereferenceable(32) %1, i8 0, i32 32, i1 false)
  %thread_ptr = call i8* asm "movq %fs:0, $0", "=r"() #3
  %ppgcstack_i8 = getelementptr i8, i8* %thread_ptr, i64 -8
  %ppgcstack = bitcast i8* %ppgcstack_i8 to {}****
  %pgcstack = load {}***, {}**** %ppgcstack, align 8
  %2 = bitcast [4 x {}*]* %gcframe2 to i64*
  store i64 8, i64* %2, align 16
  %3 = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 1
  %4 = bitcast {}** %3 to {}***
  %5 = load {}**, {}*** %pgcstack, align 8
  store {}** %5, {}*** %4, align 8
  %6 = bitcast {}*** %pgcstack to {}***
  store {}** %gcframe2.sub, {}*** %6, align 8
  %7 = load atomic {}*, {}** inttoptr (i64 139677198024920 to {}**) unordered, align 8
  %8 = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 2
  store {}* %7, {}** %8, align 16
  store {}* inttoptr (i64 139684618571936 to {}*), {}** %.sub, align 8
  %9 = getelementptr inbounds [2 x {}*], [2 x {}*]* %0, i64 0, i64 1
  store {}* %7, {}** %9, align 8
  %10 = call nonnull {}* @ijl_apply_generic({}* inttoptr (i64 139684405754928 to {}*), {}** nonnull %.sub, i32 2)
  %11 = load atomic {}*, {}** inttoptr (i64 139677192955480 to {}**) unordered, align 8
  %12 = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 3
  store {}* %10, {}** %12, align 8
  store {}* %11, {}** %8, align 16
  store {}* %10, {}** %.sub, align 8
  store {}* %11, {}** %9, align 8
  %13 = call nonnull {}* @ijl_apply_generic({}* inttoptr (i64 139684404133088 to {}*), {}** nonnull %.sub, i32 2)
  %14 = load {}*, {}** %3, align 8
  %15 = bitcast {}*** %pgcstack to {}**
  store {}* %14, {}** %15, align 8
  ret {}* %13
}

Fix 1: Work in local scope#

function local_scope()
    a = 2.0
    b = 3.0

    f() = 2 * a + b

    return f()
end

local_scope()

7.0

@code_warntype local_scope()

MethodInstance for local_scope()
  from local_scope() in Main at In[26]:1
Arguments
  #self#::Core.Const(local_scope)
Locals
  f::var"#f#7"{Float64, Float64}
  b::Float64
  a::Float64
Body::Float64
1 ─      (a = 2.0

)
│        (b = 3.0)
│   %3 = Main.:(var"#f#7")::Core.Const(var"#f#7")
│   %4 = Core.typeof(b

::Core.Const(3.0))::Core.Const(Float64)
│   %5 = Core.typeof(a::Core.Const(2.0))::Core.Const(Float64)
│   %6 = Core.apply_type(%3, %4, %5)::Core.Const(var"#f#7"{Float64, Float64})
│   %7 = b::Core.Const(3.0)
│        (f = %new(%6, %7, a::Core.Const(2.0)))
│   %9 = (f::Core.Const(var"#f#7"{Float64, Float64}(3.0, 2.0)))()::Core.Const(7.0)
└──      return %9

@code_llvm local_scope()

;  @ In[26]:1 within `local_scope`
define double @julia_local_scope_3014() #0 {
top:
  ret double 7.000000e+00
}

@code_native local_scope()

	.text
	.file	"local_scope"
	.section	.rodata.cst8,"aM",@progbits,8
	.p2align	3                               # -- Begin function julia_local_scope_3030
.LCPI0_0:
	.quad	0x401c000000000000              # double 7
	.text
	.globl	julia_local_scope_3030
	.p2align	4, 0x90
	.type	julia_local_scope_3030,@function
julia_local_scope_3030:                 # @julia_local_scope_3030
; ┌ @ In[26]:1 within `local_scope`
	.cfi_startproc
# %bb.0:                                # %top
	movabsq	$.LCPI0_0, %rax
	vmovsd	(%rax), %xmm0                   # xmm0 = mem[0],zero
	retq
.Lfunc_end0:
	.size	julia_local_scope_3030, .Lfunc_end0-julia_local_scope_3030
	.cfi_endproc
; └
                                        # -- End function
	.section	".note.GNU-stack","",@progbits

This is fast.

In fact, it’s not just fast, but as fast as it can be! Julia has figured out the result of the calculation at compile-time and returns just the literal, i.e. local_scope() = 7.

Fix 2: Make globals constant#

const C = 2.0
const D = 3.0

f() = 2 * C + D

f()

7.0

@code_llvm f()

;  @ In[30]:4 within `f`
define double @julia_f_3034() #0 {
top:
  ret double 7.000000e+00
}

@code_warntype f()

MethodInstance for f()
  from f() in Main at In[30]:4
Arguments
  #self#::Core.Const(f)
Body::Float64
1 ─ %1 = (2 * Main.C)::Core.Const(4.0)
│   %2 = (%1 + Main.D)::Core.Const(7.0)
└──      return %2

Fix 3: Write self-contained functions#

f(a, b) = 2 * a + b

f (generic function with 3 methods)

@code_llvm debuginfo=:none f(2.0, 3.0)

define double @julia_f_3042(double %0, double %1) #0 {
top:
  %2 = fmul double %0, 2.000000e+00
  %3 = fadd double %2, %1
  ret double %3
}

Write functions not scripts!

Example: Multiple Returns#

function f(x, flag)
    if flag
        return convert(Vector{Float64}, x)
    else
        return convert(Vector{Int64}, round.(x))
    end
end

f (generic function with 3 methods)

@code_warntype f(rand(10), true)

MethodInstance for f(::Vector{Float64}, ::Bool)
  from f(x, flag) in Main at In[35]:1
Arguments
  #self#::Core.Const(f)
  x::Vector{Float64}
  flag::Bool
Body::Union{Vector{Float64}, Vector{Int64}}
1 ─      goto #3 if not flag
2 ─ %2 = Core.apply_type(Main.Vector, Main.Float64)::Core.Const(Vector{Float64})
│   %3 = Main.convert(%2, x)::Vector{Float64}
└──      return %3
3 ─ %5 = Core.apply_type(Main.Vector, Main.Int64)::Core.Const(Vector{Int64})
│   %6 = Base.broadcasted(Main.round, x)::Base.Broadcast.Broadcasted{Base.Broadcast.DefaultArrayStyle{1}, Nothing, typeof(round), Tuple{Vector{Float64}}}
│   %7 = Base.materialize(%6)::Vector{Float64}
│   %8 = Main.convert(%5, %7)::Vector{Int64}
└──      return %8

typeof(f(rand(10), true))

Vector{Float64} (alias for Array{Float64, 1})

typeof(f(rand(10), false))

Vector{Int64} (alias for Array{Int64, 1})

Fix: Hint Return Type#

function f(x, flag)::Vector{Float64}
    if flag
        return 1:length(x)
    else
        return x
    end
end

f (generic function with 3 methods)

@code_warntype f(rand(10), true)

MethodInstance for f(::Vector{Float64}, ::Bool)
  from f(x, flag) in Main at In[39]:1
Arguments
  #self#::Core.Const(f)
  x::Vector{Float64}
  flag::Bool
Body::Vector{Float64}
1 ─ %1 = Core.apply_type(Main.Vector, Main.Float64)::Core.Const(Vector{Float64})
└──      goto #3 if not flag
2 ─ %3 = Main.length(x)::Int64
│   %4 = (1:%3)::Core.PartialStruct(UnitRange{Int64}, Any[Core.Const(1), Int64])

│   %5 = Base.convert(%1, %4)::Vector{Float64}
│   %6 = Core.typeassert(%5, %1)::Vector{Float64}
└──      return %6
3 ─ %8 = Base.convert(%1, x)::Vector{Float64}
│   %9 = Core.typeassert(%8, %1)::Vector{Float64}
└──      return %9

NB: Really, a Union return with a few types in it is not that bad as Julia typically handles this situation via union splitting. However it can make the compilers job harder.

Avoid Abstract Field Types#

A common reason for type inference to break are not-concretely typed fields in structs

Example 1#

using BenchmarkTools

struct MyType
    x::Number
    y::String
end

f(a::MyType) = a.x^2 + sqrt(a.x)

f (generic function with 4 methods)

a = MyType(3.0, "test")

@code_warntype f(a);

MethodInstance for f(::MyType)
  from f(a::MyType) in Main at In[42]:6
Arguments
  #self#::Core.Const(f)
  a::MyType
Body::Any
1 ─ %1 = Base.getproperty(a, :x)::Number
│   %2 = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %3 = (%2)()::Core.Const(Val{2}())
│   %4 = Base.literal_pow(Main.:^, %1, %3)::Any
│   %5 = Base.getproperty(a, :x)::Number
│   %6 = Main.sqrt(%5)::Any
│   %7 = (%4 + %6)::Any
└──      return %7

@btime f($a);

  64.450 ns (3 allocations: 48 bytes)

@code_llvm f(a);

;  @ In[42]:6 within `f`
define nonnull {}* @julia_f_3180([2 x {}*]* nocapture nonnull readonly align 8 dereferenceable(16) %0) #0 {
top:
  %1 = alloca [3 x {}*], align 8
  %gcframe2 = alloca [4 x {}*], align 16
  %gcframe2.sub = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 0
  %.sub = getelementptr inbounds [3 x {}*], [3 x {}*]* %1, i64 0, i64 0
  %2 = bitcast [4 x {}*]* %gcframe2 to i8*
  call void @llvm.memset.p0i8.i32(i8* noundef nonnull align 16 dereferenceable(32) %2, i8 0, i32 32, i1 false)
  %thread_ptr = call i8* asm "movq %fs:0, $0", "=r"() #3
  %ppgcstack_i8 = getelementptr i8, i8* %thread_ptr, i64 -8
  %ppgcstack = bitcast i8* %ppgcstack_i8 to {}****
  %pgcstack = load {}***, {}**** %ppgcstack, align 8
; ┌ @ Base.jl:38 within `getproperty`
   %3 = bitcast [4 x {}*]* %gcframe2 to i64*
   store i64 8, i64* %3, align 16
   %4 = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 1
   %5 = bitcast {}** %4 to {}***
   %6 = load {}**, {}*** %pgcstack, align 8
   store {}** %6, {}*** %5, align 8
   %7 = bitcast {}*** %pgcstack to {}***
   store {}** %gcframe2.sub, {}*** %7, align 8
   %8 = getelementptr inbounds [2 x {}*], [2 x {}*]* %0, i64 0, i64 0
   %9 = load atomic {}*, {}** %8 unordered, align 8
; └
  store {}* inttoptr (i64 139684404978672 to {}*), {}** %.sub, align 8
  %10 = getelementptr inbounds [3 x {}*], [3 x {}*]* %1, i64 0, i64 1
  store {}* %9, {}** %10, align 8
  %11 = getelementptr inbounds [3 x {}*], [3 x {}*]* %1, i64 0, i64 2
  store {}* inttoptr (i64 139684412094416 to {}*), {}** %11, align 8
  %12 = call nonnull {}* @ijl_apply_generic({}* inttoptr (i64 139684404980240 to {}*), {}** nonnull %.sub, i32 3)
  %13 = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 3
  store {}* %12, {}** %13, align 8
  store {}* %9, {}** %.sub, align 8
  %14 = call nonnull {}* @ijl_apply_generic({}* inttoptr (i64 139684412113840 to {}*), {}** nonnull %.sub, i32 1)
  %15 = getelementptr inbounds [4 x {}*], [4 x {}*]* %gcframe2, i64 0, i64 2
  store {}* %14, {}** %15, align 16
  store {}* %12, {}** %.sub, align 8
  store {}* %14, {}** %10, align 8
  %16 = call nonnull {}* @ijl_apply_generic({}* inttoptr (i64 139684404133088 to {}*), {}** nonnull %.sub, i32 2)
  %17 = load {}*, {}** %4, align 8
  %18 = bitcast {}*** %pgcstack to {}**
  store {}* %17, {}** %18, align 8
  ret {}* %16
}

typeof(a)

MyType

“Type stability”: A function f is type stable if for a given set of input argument types the return type is always the same and concrete.

Fix 1: Concrete typing#

struct MyTypeConcrete
    x::Float64
    y::String
end

f(b::MyTypeConcrete) = b.x^2 + sqrt(b.x)

f (generic function with 5 methods)

b = MyTypeConcrete(3.0, "test")
@code_warntype f(b)

MethodInstance for f(::MyTypeConcrete)
  from f(b::MyTypeConcrete) in Main at In[47]:6
Arguments
  #self#::Core.Const(f)
  b::MyTypeConcrete
Body::Float64
1 ─ %1 = Base.getproperty(b, :x)::Float64
│   %2 = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %3 = (%2)()::Core.Const(Val{2}())
│   %4 = Base.literal_pow(Main.:^, %1, %3)::Float64
│   %5 = Base.getproperty(b, :x)::Float64
│   %6 = Main.sqrt(%5)::Float64
│   %7 = (%4 + %6)::Float64
└──      return %7

@btime f($b);

  3.803 ns (0 allocations: 0 bytes)

@code_llvm f(b)

;  @ In[47]:6 within `f`
define double @julia_f_3194({ double, {}* }* nocapture nonnull readonly align 8 dereferenceable(16) %0) #0 {
top:
; ┌ @ Base.jl:38 within `getproperty`
   %1 = getelementptr inbounds { double, {}* }, { double, {}* }* %0, i64 0, i32 0
; └
; ┌ @ intfuncs.jl:321 within `literal_pow`
; │┌ @ float.jl:385 within `*`
    %2 = load double, double* %1, align 8
; └└
; ┌ @ math.jl:591 within `sqrt`
; │┌ @ float.jl:412 within `<`
    %3 = fcmp uge double %2, 0.000000e+00
; │└
   br i1 %3, label %L8, label %L6

L6:                                               ; preds = %top
   %4 = call nonnull {}* @j_throw_complex_domainerror_3196({}* inttoptr (i64 139684618925992 to {}*), double %2) #0
   call void @llvm.trap()
   unreachable

L8:                                               ; preds = %top
; └
; ┌ @ intfuncs.jl:321 within `literal_pow`
; │┌ @ float.jl:385 within `*`
    %5 = fmul double %2, %2
; └└
; ┌ @ math.jl:592 within `sqrt`
   %6 = call double @llvm.sqrt.f64(double %2)
; └
; ┌ @ float.jl:383 within `+`
   %7 = fadd double %5, %6
; └
  ret double %7
}

Fix 2: Type parameters#

But what if I want to accept any kind of, say, Number and AbstractString for our type?

struct MyTypeParametric{A <: Number, B <: AbstractString}
    x::A
    y::B
end

f(c::MyTypeParametric) = c.x^2 + sqrt(c.x)

f (generic function with 6 methods)

c = MyTypeParametric(3.0, "test")

MyTypeParametric{Float64, String}(3.0, "test")

@code_warntype f(c)

MethodInstance for f(::MyTypeParametric{Float64, String})
  from f(c::MyTypeParametric) in Main at In[51]:6
Arguments
  #self#::Core.Const(f)
  c::MyTypeParametric{Float64, String}
Body::Float64
1 ─ %1 = Base.getproperty(c, :x)::Float64
│   %2 = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %3 = (%2)()::Core.Const(Val{2}())
│   %4 = Base.literal_pow(Main.:^, %1, %3)::Float64
│   %5 = Base.getproperty(c, :x)::Float64
│   %6 = Main.sqrt(%5)::Float64
│   %7 = (%4 + %6)::Float64
└──      return %7

From the type alone the compiler knows what the structure contains and can produce optimal code:

@btime f($c);

  3.812 ns (0 allocations: 0 bytes)

c = MyTypeParametric(Float32(3.0), SubString("test"))

MyTypeParametric{Float32, SubString{String}}(3.0f0, "test")

@btime f($c);

  3.344 ns (0 allocations: 0 bytes)

Example 2 - Cooler Diagonal Matrix#

Yesterday we created a diagonal matrix which could take in a Vector and create an object that acted like a diagonal matrix.

By replacing the Vector with an AbstractVector, we made this work with anything vector-like, like ranges.

However, this ended up being slower than the original implementation:

struct DiagonalMatrix{T} <: AbstractArray{T,2}
    diag::Vector{T}
end

Base.size(D::DiagonalMatrix) = (length(D.diag), length(D.diag))

function Base.getindex(D::DiagonalMatrix, i::Int, j::Int)
    if i == j
        return D.diag[i]
    else
        return zero(eltype(D))
    end
end

Base.:+(Da::DiagonalMatrix, Db::DiagonalMatrix) = DiagonalMatrix(Da.diag + Db.diag)

struct CoolerDiagonalMatrix{T} <: AbstractArray{T, 2}
    diag::AbstractVector{T}
end

Base.size(D::CoolerDiagonalMatrix) = (length(D.diag), length(D.diag))

function Base.getindex(D::CoolerDiagonalMatrix, i::Int, j::Int)
    if i == j
        return D.diag[i]
    else
        return zero(eltype(D))
    end
end

Base.:+(Da::CoolerDiagonalMatrix, Db::CoolerDiagonalMatrix) = CoolerDiagonalMatrix(Da.diag + Db.diag)

DM = DiagonalMatrix(collect(1:100))
@btime $DM + $DM

DM_cool = CoolerDiagonalMatrix(collect(1:100))
@btime $DM_cool + $DM_cool;

  85.082 ns (1 allocation: 896 bytes)

  186.628 ns (2 allocations: 912 bytes)

@code_warntype DM + DM

MethodInstance for +(::DiagonalMatrix{Int64}, ::DiagonalMatrix{Int64})
  from +(Da::DiagonalMatrix, Db::DiagonalMatrix) in Main at In[57]:15
Arguments
  #self#::Core.Const(+)
  Da::DiagonalMatrix{Int64}
  Db::DiagonalMatrix{Int64}
Body::DiagonalMatrix{Int64}
1 ─ %1 = Base.getproperty(Da, :diag)::Vector{Int64}
│   %2 = Base.getproperty(Db, :diag)::Vector{Int64}
│   %3 = (%1 + %2)::Vector{Int64}
│   %4 = Main.DiagonalMatrix(%3)::DiagonalMatrix{Int64}
└──      return %4

@code_warntype DM_cool + DM_cool

MethodInstance for +(::CoolerDiagonalMatrix{Int64}, ::CoolerDiagonalMatrix{Int64})
  from +(Da::CoolerDiagonalMatrix, Db::CoolerDiagonalMatrix) in Main at In[58]:15
Arguments
  #self#::Core.Const(+)
  Da::CoolerDiagonalMatrix{Int64}
  Db::CoolerDiagonalMatrix{Int64}
Body::CoolerDiagonalMatrix
1 ─ %1 = Base.getproperty(Da, :diag)::AbstractVector{Int64}
│   %2 = Base.getproperty(Db, :diag)::AbstractVector{Int64}
│   %3 = (%1 + %2)::Any
│   %4 = Main.CoolerDiagonalMatrix(%3)::CoolerDiagonalMatrix
└──      return %4

This is the same as the previous problem: an AbstractVector{Int64} is not a concrete type, it means:

subtypes(AbstractVector{Int64})

14-element Vector{Any}:
 AbstractRange{Int64}
 Base.LogicalIndex{Int64}
 Base.ReinterpretArray{Int64, 1, S} where S
 Base.ReshapedArray{Int64, 1}
 Core.Compiler.AbstractRange{Int64}
 Core.Compiler.LinearIndices{1, R} where R<:Tuple{Core.Compiler.AbstractUnitRange{Int64}}
 DenseVector{Int64} (alias for DenseArray{Int64, 1})
 LinearIndices{1, R} where R<:Tuple{AbstractUnitRange{Int64}}
 PermutedDimsArray{Int64, 1}
 AbstractSparseVector{Int64} (alias for SparseArrays.AbstractSparseArray{Int64, Ti, 1} where Ti)
 StaticArrays.TrivialView{A, Int64, 1} where A
 StaticArray{S, Int64, 1} where S<:Tuple
 SubArray{Int64, 1}
 Test.GenericArray{Int64, 1}

So really it’s a union of all of the above types, not a single type!

We can avoid this with some slightly fancier code:

struct MuchCoolerDiagonalMatrix{T, U <: AbstractVector} <: AbstractArray{T, 2}
    diag::U
end

Base.size(D::MuchCoolerDiagonalMatrix) = (length(D.diag), length(D.diag))

function Base.getindex(D::MuchCoolerDiagonalMatrix, i::Int, j::Int)
    if i == j
        return D.diag[i]
    else
        return zero(eltype(D))
    end
end

Base.:+(Da::MuchCoolerDiagonalMatrix, Db::MuchCoolerDiagonalMatrix) = MuchCoolerDiagonalMatrix(Da.diag + Db.diag)

MuchCoolerDiagonalMatrix(1:10)

MethodError: no method matching MuchCoolerDiagonalMatrix(::UnitRange{Int64})

Stacktrace:
 [1] top-level scope
   @ In[64]:1

typeof(1:10)

UnitRange{Int64}

MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}(1:10)

10×10 MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}:
 1  0  0  0  0  0  0  0  0   0
 0  2  0  0  0  0  0  0  0   0
 0  0  3  0  0  0  0  0  0   0
 0  0  0  4  0  0  0  0  0   0
 0  0  0  0  5  0  0  0  0   0
 0  0  0  0  0  6  0  0  0   0
 0  0  0  0  0  0  7  0  0   0
 0  0  0  0  0  0  0  8  0   0
 0  0  0  0  0  0  0  0  9   0
 0  0  0  0  0  0  0  0  0  10

MuchCoolerDiagonalMatrix(diag::AbstractVector) = MuchCoolerDiagonalMatrix{eltype(diag), typeof(diag)}(diag)

MuchCoolerDiagonalMatrix

MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}(1:10)

10×10 MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}:
 1  0  0  0  0  0  0  0  0   0
 0  2  0  0  0  0  0  0  0   0
 0  0  3  0  0  0  0  0  0   0
 0  0  0  4  0  0  0  0  0   0
 0  0  0  0  5  0  0  0  0   0
 0  0  0  0  0  6  0  0  0   0
 0  0  0  0  0  0  7  0  0   0
 0  0  0  0  0  0  0  8  0   0
 0  0  0  0  0  0  0  0  9   0
 0  0  0  0  0  0  0  0  0  10

DM = DiagonalMatrix(collect(1:100))
@btime $DM + $DM

DM_cool = CoolerDiagonalMatrix(collect(1:100))
@btime $DM_cool + $DM_cool;

DM_mcool = MuchCoolerDiagonalMatrix(collect(1:100))
@btime $DM_mcool + $DM_mcool;

  84.021 ns (1 allocation: 896 bytes)

  184.630 ns (2 allocations: 912 bytes)

  86.395 ns (1 allocation: 896 bytes)

DM = DiagonalMatrix(collect(1:100))
@btime $DM + $DM

DM_cool = CoolerDiagonalMatrix(1:100)
@btime $DM_cool + $DM_cool;

DM_mcool = MuchCoolerDiagonalMatrix(1:100)
@btime $DM_mcool + $DM_mcool;

  84.281 ns (1 allocation: 896 bytes)

  122.159 ns (3 allocations: 112 bytes)

  12.050 ns (0 allocations: 0 bytes)

@code_warntype DM_mcool + DM_mcool

MethodInstance for +(::MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}, ::MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}})
  from +(Da::MuchCoolerDiagonalMatrix, Db::MuchCoolerDiagonalMatrix) in Main at In[63]:15
Arguments
  #self#::Core.Const(+)
  Da::MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}
  Db::MuchCoolerDiagonalMatrix{Int64, UnitRange{Int64}}
Body::MuchCoolerDiagonalMatrix{Int64, StepRangeLen{Int64, Int64, Int64, Int64}}
1 ─ %1 = Base.getproperty(Da, :diag)::UnitRange{Int64}
│   %2 = Base.getproperty(Db, :diag)::UnitRange{Int64}
│   %3 = (%1 + %2)::Core.PartialStruct(StepRangeLen{Int64, Int64, Int64, Int64}, Any[Int64, Core.Const(2), Int64, Core.Const(1)])
│   %4 = Main.MuchCoolerDiagonalMatrix(%3)::Core.PartialStruct(MuchCoolerDiagonalMatrix{Int64, StepRangeLen{Int64, Int64, Int64, Int64}}, Any[Core.PartialStruct(StepRangeLen{Int64, Int64, Int64, Int64}, Any[Int64, Core.Const(2), Int64, Core.Const(1)])])
└──      return %4

Avoid Untyped Containers#

Example#

function f()
    numbers = []
    for i in 1:10
        push!(numbers, i)
    end
    sum(numbers)
end

@btime f();

  301.373 ns (3 allocations: 464 bytes)

@code_warntype f()

MethodInstance for f()
  from f() in Main at In[72]:1
Arguments
  #self#::Core.Const(f)
Locals
  @_2::Union{Nothing, Tuple{Int64, Int64}}
  numbers::Vector{Any}
  i::Int64
Body::Any
1 ─       (numbers = Base.vect())
│   %2  = (1:10)::Core.Const(1:10)
│         (@_2 = Base.iterate(%2))
│   %4  = (@_2::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %5  = Base.not_int(%4)::Core.Const(true)
└──       goto #4 if not %5
2 ┄ %7  = @_2::Tuple{Int64, Int64}
│         (i = Core.getfield(%7, 1))
│   %9  = Core.getfield(%7, 2)::Int64
│         Main.push!(numbers, i)
│         (@_2 = Base.iterate(%2, %9))
│   %12 = (@_2 === nothing)::Bool
│   %13 = Base.not_int(%12)::Bool
└──       goto #4 if not %13
3 ─       goto #2
4 ┄ %16 = Main.sum(numbers)::Any
└──       return %16

typeof([])

Vector{Any} (alias for Array{Any, 1})

function f()
    numbers = Int[]
    for i in 1:10
        push!(numbers, i)
    end
    sum(numbers)
end

@btime f();

  155.269 ns (3 allocations: 480 bytes)

@code_warntype f()

MethodInstance for f()
  from f() in Main at In[75]:1
Arguments
  #self#::Core.Const(f)
Locals
  @_2::Union{Nothing, Tuple{Int64, Int64}}
  numbers::Vector{Int64}
  i::Int64
Body::Int64
1 ─       (numbers = Base.getindex(Main.Int))
│   %2  = (1:10)::Core.Const(1:10)
│         (@_2 = Base.iterate(%2))
│   %4  = (@_2::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %5  = Base.not_int(%4)::Core.Const(true)
└──       goto #4 if not %5
2 ┄ %7  = @_2::Tuple{Int64, Int64}
│         (i = Core.getfield(%7, 1))
│   %9  = Core.getfield(%7, 2)::Int64
│         Main.push!(numbers, i)
│         (@_2 = Base.iterate(%2, %9))
│   %12 = (@_2 === nothing)::Bool
│   %13 = Base.not_int(%12)::Bool
└──       goto #4 if not %13
3 ─       goto #2
4 ┄ %16 = Main.sum(numbers)::Int64
└──       return %16

Avoid Changing Variable Types#

Variables in a function should not change type.

Example#

function f()
    x = 1
    for i = 1:10
        x /= rand()
    end
    return x
end

@code_warntype f();

MethodInstance for f()
  from f() in Main at In[77]:1
Arguments
  #self#::Core.Const(f)
Locals
  @_2::Union{Nothing, Tuple{Int64, Int64}}
  x::Union{Float64, Int64}
  i::Int64
Body::Float64
1 ─       (x = 1)
│   %2  = (1:10)::Core.Const(1:10)
│         (@_2 = Base.iterate(%2))
│   %4  = (@_2::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %5  = Base.not_int(%4)::Core.Const(true)
└──       goto #4 if not %5
2 ┄ %7  = @_2::Tuple{Int64, Int64}
│         (i = Core.getfield(%7, 1))
│   %9  = Core.getfield(%7, 2)::Int64
│   %10 = x::Union{Float64, Int64}
│   %11 = Main.rand()::Float64
│         (x = %10 / %11)
│         (@_2 = Base.iterate(%2, %9))
│   %14 = (@_2 === nothing)::Bool
│   %15 = Base.not_int(%14)::Bool
└──       goto #4 if not %15
3 ─       goto #2
4 ┄       return x::Float64

(On a side note: since the type can only vary between Float64 and Int64, Julia can still produce reasonable code by union splitting. I recommend reading this blog post by Tim Holy.)

Fix 1: Initialize with correct type#

function f()
    x = 1.0
    for i = 1:10
        x /= rand()
    end
    return x
end

@code_warntype f()

MethodInstance for f()
  from f() in Main at In[78]:1
Arguments
  #self#::Core.Const(f)
Locals
  @_2::Union{Nothing, Tuple{Int64, Int64}}
  x::Float64
  i::Int64
Body::Float64
1 ─       (x = 1.0)
│   %2  = (1:10)::Core.Const(1:10)
│         (@_2 = Base.iterate(%2))
│   %4  = (@_2::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %5  = Base.not_int(%4)::Core.Const(true)
└──       goto #4 if not %5
2 ┄ %7  = @_2::Tuple{Int64, Int64}
│         (i = Core.getfield(%7, 1))
│   %9  = Core.getfield(%7, 2)::Int64
│   %10 = x::Float64
│   %11 = Main.rand()::Float64
│         (x = %10 / %11)
│         (@_2 = Base.iterate(%2, %9))
│   %14 = (@_2 === nothing)::Bool
│   %15 = Base.not_int(%14)::Bool
└──       goto #4 if not %15
3 ─       goto #2
4 ┄       return x

Fix 2: Specify types (to get errors or to heal the problem by conversion)#

function f()
    x::Float64 = 1 # implicit conversion
    for i = 1:10
        x /= rand()
    end
    return x
end

@code_warntype f()

MethodInstance for f()
  from f() in Main at In[79]:1
Arguments
  #self#::Core.Const(f)
Locals
  @_2::Union{Nothing, Tuple{Int64, Int64}}
  x::Float64
  i::Int64
Body::Float64
1 ─ %1  = Base.convert(Main.Float64, 1)::Core.Const(1.0)
│         (x = Core.typeassert(%1, Main.Float64))
│   %3  = (1:10)::Core.Const(1:10)
│         (@_2 = Base.iterate(%3))
│   %5  = (@_2::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %6  = Base.not_int(%5)::Core.Const(true)
└──       goto #4 if not %6
2 ┄ %8  = @_2::Tuple{Int64, Int64}
│         (i = Core.getfield(%8, 1))
│   %10 = Core.getfield(%8, 2)::Int64
│   %11 = x::Float64
│   %12 = Main.rand()::Float64
│   %13 = (%11 / %12)::Float64
│   %14 = Base.convert(Main.Float64, %13)::Float64
│         (x = Core.typeassert(%14, Main.Float64))
│         (@_2 = Base.iterate(%3, %10))
│   %17 = (@_2 === nothing)::Bool
│   %18 = Base.not_int(%17)::Bool
└──       goto #4 if not %18
3 ─       goto #2
4 ┄       return x

Fix 3: Special-case first iteration#

function f()
    x = 1 / rand()
    for i = 2:10
        x /= rand()
    end
    return x
end

@code_warntype f()

MethodInstance for f()
  from f() in Main at In[80]:1
Arguments
  #self#::Core.Const(f)
Locals
  @_2::Union{Nothing, Tuple{Int64, Int64}}
  x::Float64
  i::Int64
Body::Float64
1 ─ %1  = Main.rand()::Float64
│         (x = 1 / %1)
│   %3  = (2:10)::Core.Const(2:10)
│         (@_2 = Base.iterate(%3))
│   %5  = (@_2::Core.Const((2, 2)) === nothing)::Core.Const(false)
│   %6  = Base.not_int(%5)::Core.Const(true)
└──       goto #4 if not %6
2 ┄ %8  = @_2::Tuple{Int64, Int64}
│         (i = Core.getfield(%8, 1))
│   %10 = Core.getfield(%8, 2)::Int64
│   %11 = x::Float64
│   %12 = Main.rand()::Float64
│         (x = %11 / %12)
│         (@_2 = Base.iterate(%3, %10))
│   %15 = (@_2 === nothing)::Bool
│   %16 = Base.not_int(%15)::Bool
└──       goto #4 if not %16
3 ─       goto #2
4 ┄       return x

Isolate Unavoidable Type Instabilities#

Type instabilities can occur very naturally, for example when reading unknown user files or user input. Hence, not every instability can be avoided.

If that’s the case, isolate your expensive computation from the instability by putting it in a separate kernel function (also known as introducing a function barrier).

data = Union{Int64,Float64,String}[4, 2.0, "test", 3.2, 1]

5-element Vector{Union{Float64, Int64, String}}:
 4
 2.0
  "test"
 3.2
 1

function computation(data)
    x = 1.0
    for i in 1:100
        x = sin(data[1])
        x += data[2]
        x *= data[4]
    end
    return x
end

@code_warntype computation(data)

MethodInstance for computation(::Vector{Union{Float64, Int64, String}})
  from computation(data) in Main at In[82]:1
Arguments
  #self#::Core.Const(computation)
  data::Vector{Union{Float64, Int64, String}}
Locals
  @_3::Union{Nothing, Tuple{Int64, Int64}}
  x::Float64
  i::Int64
Body::Float64
1 ─       (x = 1.0)
│   %2  = (1:100)::Core.Const(1:100)
│         (@_3 = Base.iterate(%2))
│   %4  = (@_3::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %5  = Base.not_int(%4)::Core.Const(true)
└──       goto #4 if not %5
2 ┄ %7  = @_3::Tuple{Int64, Int64}
│         (i = Core.getfield(%7, 1))
│   %9  = Core.getfield(%7, 2)::Int64
│   %10 = Base.getindex(data, 1)::Union{Float64, Int64, String}
│         (x = Main.sin(%10))
│   %12 = x::Float64
│   %13 = Base.getindex(data, 2)::Union{Float64, Int64, String}
│         (x = %12 + %13)
│   %15 = x::Float64
│   %16 = Base.getindex(data, 4)::Union{Float64, Int64, String}
│         (x = %15 * %16)
│         (@_3 = Base.iterate(%2, %9))
│   %19 = (@_3 === nothing)::Bool
│   %20 = Base.not_int(%19)::Bool
└──       goto #4 if not %20
3 ─       goto #2
4 ┄       return x

@btime computation($data);

  1.256 μs (0 allocations: 0 bytes)

function computation(data)
    a = data[1]
    b = data[2]
    c = data[4]
    return _computation_kernel(a, b, c)
end

function _computation_kernel(a, b, c)
    x = 1.0
    for i in 1:100
        x = sin(a)
        x += b
        x *= c
    end
    return x
end

_computation_kernel (generic function with 1 method)

@code_warntype computation(data)

MethodInstance for computation(::Vector{Union{Float64, Int64, String}})
  from computation(data) in Main

 at In[84]:1
Arguments
  #self#::Core.Const(computation)
  data::Vector{Union{Float64, Int64, String}}
Locals
  c::Union{Float64, Int64, String}
  b::Union{Float64, Int64, String}
  a::Union{Float64, Int64, String}
Body::Float64
1 ─      (a = Base.getindex(data, 1))
│        (b = Base.getindex(data, 2))
│        (c = Base.getindex(data, 4))
│   %4 = Main._computation_kernel(a, b, c)::Float64
└──      return %4

@code_warntype _computation_kernel(data[1], data[2], data[4])

MethodInstance for _computation_kernel(::Int64, ::Float64, ::Float64)
  from _computation_kernel(a, b, c) in Main at In[84]:8
Arguments
  #self#::Core.Const(_computation_kernel)
  a::Int64
  b::Float64
  c::Float64
Locals
  @_5::Union{Nothing, Tuple{Int64, Int64}}
  x::Float64
  i::Int64
Body::Float64
1 ─       (x = 1.0)
│   %2  = (1:100)::Core.Const(1:100)
│         (@_5 = Base.iterate(%2))
│   %4  = (@_5::Core.Const((1, 1)) === nothing)::Core.Const(false)
│   %5  = Base.not_int(%4)::Core.Const(true)
└──       goto #4 if not %5
2 ┄ %7  = @_5::Tuple{Int64, Int64}
│         (i = Core.getfield(%7, 1))
│   %9  = Core.getfield(%7, 2)::Int64
│         (x = Main.sin(a))
│         (x = x + b)
│         (x = x * c)
│         (@_5 = Base.iterate(%2, %9))
│   %14 = (@_5 === nothing)::Bool
│   %15 = Base.not_int(%14)::Bool
└──       goto #4 if not %15
3 ─       goto #2
4 ┄       return x

@btime computation($data);

  938.464 ns (1 allocation: 16 bytes)

Note that the computational kernel function is fully type inferred.

Access Arrays in Column-Major Order#

Excellent page on this topic: https://book.sciml.ai/notes/02-Optimizing_Serial_Code/

Fastest varying loop index goes first.

function fcol!(M)
    for col in 1:size(M, 2)
        for row in 1:size(M, 1)
            M[row, col] = 42
        end
    end
    nothing
end

function frow!(M)
    for row in 1:size(M, 1)
        for col in 1:size(M, 2)
            M[row, col] = 42
        end
    end
    nothing
end

frow! (generic function with 1 method)

@benchmark fcol!(A) setup=(A=Array{Int64, 2}(undef, 1000, 1000))

BenchmarkTools.Trial: 4905 samples with 1 evaluation.
 Range (min … max):  687.379 μs …   2.519 ms  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     734.717 μs               ┊ GC (median):    0.00%
 Time  (mean ± σ):   866.176 μs ± 315.315 μs  ┊ GC (mean ± σ):  0.00% ± 0.00%

  ▄▇█▇▃                            ▃▂▂▂                    ▂▃▃▂ ▁
  █████▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆██████▄▃▁▁▃▁▁▁▁▁▁▁▃▄▁▅▅▅█████ █
  687 μs        Histogram: log(frequency) by time       1.78 ms <

 Memory estimate: 0 bytes, allocs estimate: 0.

@benchmark frow!(A) setup=(A=Array{Int64, 2}(undef, 1000, 1000))

BenchmarkTools.Trial: 1974 samples with 1 evaluation.
 Range (min … max):  2.214 ms …   4.209 ms  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     2.257 ms               ┊ GC (median):    0.00%
 Time  (mean ± σ):   2.383 ms ± 331.395 μs  ┊ GC (mean ± σ):  0.00% ± 0.00%

  ▇█▇▅        ▁▁         ▁                                     
  ████▅▃▃▁▃▄▆▆███▇▆▆▅▄▅▅▇█▇▅▁▃▃▃▃▁▁▃▃▁▁▁▁▄▃▅▇▇▆▇▆▇▇█▇▆▆▇██▇▆▃ █
  2.21 ms      Histogram: log(frequency) by time      3.53 ms <

 Memory estimate: 0 bytes, allocs estimate: 0.

Lots of cache misses for frow!

Performance Annotations#

@inbounds#

Disables bounds checks. (Julia may segfault if you use it wrongly!)

function f()
    x = [1, 2, 3]
    for i in 1:100_000
        for k in 1:3
            x[k] = x[k] + 2 * x[k]
        end
    end
    return x
end

@btime f();

  200.578 μs (1 allocation: 80 bytes)

function f_inbounds()
    x = [1, 2, 3]
    for i in 1:100_000
        for k in 1:3
            @inbounds x[k] = x[k] + 2 * x[k]
        end
    end
    return x
end

@btime f_inbounds();

  501.244 μs (1 allocation: 80 bytes)

@simd#

Enables SIMD optimizations that are potentially unsafe. Julia may execute loop iterations in arbitrary or overlapping order.

x = rand(1000);

function f(x)
    s = zero(eltype(x))
    for i in x
        s += i
    end
    return s
end

@btime f($x);

  1.294 μs (0 allocations: 0 bytes)

function f_simd(x)
    s = zero(eltype(x))
    @simd for i in x
        s += i
    end
    return s
end

@btime f_simd($x);

  102.782 ns (0 allocations: 0 bytes)

(For integer input both versions have the same speed because integer addition is associative, in contrast to floating point arithmetics.)

using CpuId
cpuinfo()

| Cpu Property | Value | |:------------------ |:---------------------------------------------------------- | | Brand | Intel(R) Xeon(R) Silver 4214R CPU @ 2.40GHz | | Vendor | :Intel | | Architecture | :Skylake | | Model | Family: 0x06, Model: 0x55, Stepping: 0x07, Type: 0x00 | | Cores | 12 physical cores, 24 logical cores (on executing CPU) | | | Hyperthreading hardware capability detected | | Clock Frequencies | 2400 / 3500 MHz (base/max), 100 MHz bus | | Data Cache | Level 1:3 : (32, 1024, 16896) kbytes | | | 64 byte cache line size | | Address Size | 48 bits virtual, 46 bits physical | | SIMD | 512 bit = 64 byte max. SIMD vector size | | Time Stamp Counter | TSC is accessible via rdtsc | | | TSC runs at constant rate (invariant from clock frequency) | | Perf. Monitoring | Performance Monitoring Counters (PMC) revision 4 | | | Available hardware counters per logical core: | | | 3 fixed-function counters of 48 bit width | | | 4 general-purpose counters of 48 bit width | | Hypervisor | No |

x = rand(Float32, 1000);

@btime f($x);
@btime f_simd($x);

  1.294 μs (0 allocations: 0 bytes)

  58.511 ns (0 allocations: 0 bytes)

@fastmath#

Enables lots of floating point optimizations that are potentially unsafe! It trades accuracy for speed, so, Beware of fast-math. (See the LLVM Language Reference Manual for more information on which compiler options it sets.)

There is julia --math-mode=fast to enable fast math globally.

Harmless example: FMA - Fused Multiply Add

@noinline f(a, b, c) = a * b + c

@code_native debuginfo=:none f(1.0, 2.0, 3.0)

	.text
	.file	"f"
	.globl	julia_f_4875                    # -- Begin function julia_f_4875
	.p2align	4, 0x90
	.type	julia_f_4875,@function
julia_f_4875:                           # @julia_f_4875
	.cfi_startproc
# %bb.0:                                # %top
	vmulsd	%xmm1, %xmm0, %xmm0
	vaddsd	%xmm2, %xmm0, %xmm0
	retq
.Lfunc_end0:
	.size	julia_f_4875, .Lfunc_end0-julia_f_4875
	.cfi_endproc
                                        # -- End function
	.section	".note.GNU-stack","",@progbits

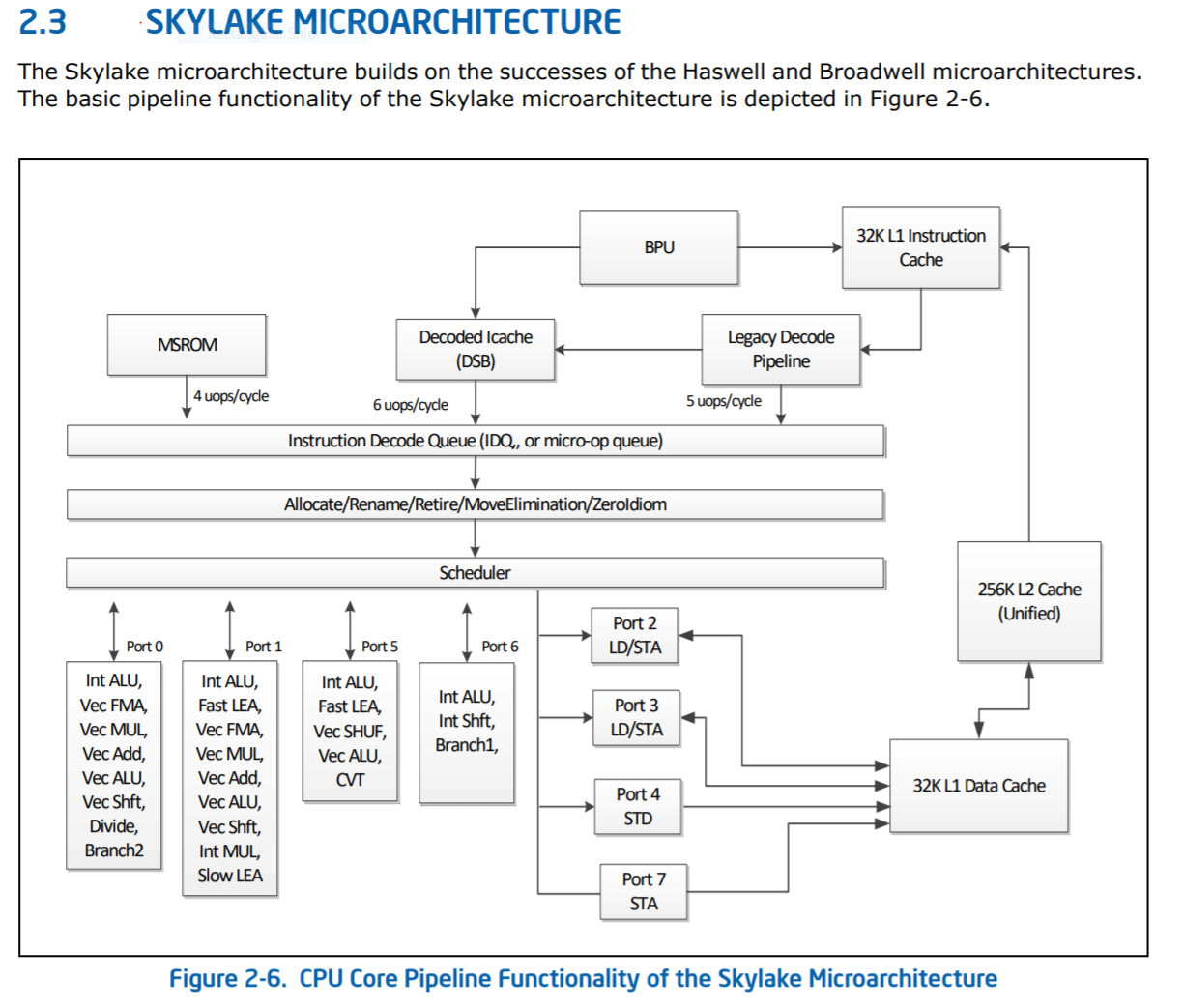
Source: Intel® 64 and IA-32 Architectures Optimization Reference Manual

f_fma(a, b, c) = fma(a, b, c)

@code_native debuginfo=:none f_fma(1.0, 2.0, 3.0)

	.text
	.file	"f_fma"
	.globl	julia_f_fma_4877                # -- Begin function julia_f_fma_4877
	.p2align	4, 0x90
	.type	julia_f_fma_4877,@function
julia_f_fma_4877:                       # @julia_f_fma_4877
	.cfi_startproc
# %bb.0:                                # %L7
	vfmadd213sd	%xmm2, %xmm1, %xmm0     # xmm0 = (xmm1 * xmm0) + xmm2
	retq
.Lfunc_end0:
	.size	julia_f_fma_4877, .Lfunc_end0-julia_f_fma_4877
	.cfi_endproc
                                        # -- End function
	.section	".note.GNU-stack","",@progbits

f_fastmath(a, b, c) = @fastmath a * b + c

@code_native debuginfo=:none f_fastmath(1.0, 2.0, 3.0)

	.text
	.file	"f_fastmath"
	.globl	julia_f_fastmath_4881           # -- Begin function julia_f_fastmath_4881
	.p2align	4, 0x90
	.type	julia_f_fastmath_4881,@function
julia_f_fastmath_4881:                  # @julia_f_fastmath_4881
	.cfi_startproc
# %bb.0:                                # %top
	vfmadd213sd	%xmm2, %xmm1, %xmm0     # xmm0 = (xmm1 * xmm0) + xmm2
	retq
.Lfunc_end0:
	.size	julia_f_fastmath_4881, .Lfunc_end0-julia_f_fastmath_4881
	.cfi_endproc
                                        # -- End function
	.section	".note.GNU-stack","",@progbits

Benchmarking this probably won’s show a difference due to the noise on the system dominating the tiny benefits of saving one instruction.

We get into this later

(P.S. In this specific case, MuladdMacro.jl is a safe alternative.

CPU operations vary in cost#

http://ithare.com/infographics-operation-costs-in-cpu-clock-cycles/

Example: Division vs multiplication#

div(x) = x ./ 1000
mul(x) = x .* 1e-3

mul (generic function with 1 method)

x = rand(1000)

@btime $x ./ 1000;
@btime $x .* 1e-3;

  913.161 ns (1 allocation: 7.94 KiB)

  800.786 ns (1 allocation: 7.94 KiB)

Analysis Tools#

Traceur.jl#

Basic automatic performance trap checker. Essentially a codified version of the performance tips in the Julia documentation.

Important macro: @trace

using Traceur

a = 2.0
b = 3.0

f() = 2 * a + b

@trace f()

┌ Warning: uses global variable Main.a
└ @ In[103]:6
┌ Warning: uses global variable Main.b
└ @ In[103]:6
┌ Warning: dynamic dispatch to 2 * Main.a
└ @ In[103]:6
┌ Warning: dynamic dispatch to 2 * Main.a + Main.b
└ @ In[103]:6
┌ Warning: f returns Any
└ @ In[103]:6

7.0

JET.jl#

Static code analyzer. (Doesn’t execute the code!)

Important macros:

using JET

a = 2.0
b = 3.0

f() = 2 * a + b

@report_opt f() # check for possible optimization problems

═════ 2 possible errors found ═════
┌ @ In[104]:6 2 * %1
│ runtime dispatch detected: (2 * %1::Any)::Any
└─────────────
┌ @ In[104]:6 %2 + %3
│ runtime dispatch detected: (%2::Any + %3::Any)::Any
└─────────────

f() = x + 2

@report_call f() # check for possible errors

No errors detected

@report_opt f()

═════ 1 possible error found ═════
┌ @ In[105]:1 %1 + 2
│ runtime dispatch detected: (%1::Any + 2)::Any
└─────────────

@report_call sum("Hamburg")

═════ 2 possible errors found ═════
┌ @ reduce.jl:557 Base.:(var"#sum#267")(pairs(NamedTuple()), #self#, a)
│┌ @ reduce.jl:557 sum(identity, a)
││┌ @ reduce.jl:528 Base.:(var"#sum#266")(pairs(NamedTuple()), #self#, f, a)
│││┌ @ reduce.jl:528 mapreduce(f, Base.add_sum, a)
││││┌ @ reduce.jl:302 Base.:(var"#mapreduce#263")(pairs(NamedTuple()), #self#, f, op, itr)
│││││┌ @ reduce.jl:302 mapfoldl(f, op, itr)
││││││┌ @ reduce.jl:170 Base.:(var"#mapfoldl#259")(Base._InitialValue(), #self#, f, op, itr)
│││││││┌ @ reduce.jl:170 Base.mapfoldl_impl(f, op, init, itr)
││││││││┌ @ reduce.jl:44 Base.foldl_impl(op′, nt, itr′)
│││││││││┌ @ reduce.jl:48 v = Base._foldl_impl(op, nt, itr)
││││││││││┌ @ reduce.jl:62 v = op(v, y[1])
│││││││││││┌ @ reduce.jl:81 op.rf(acc, x)
││││││││││││┌ @ reduce.jl:24 x + y
│││││││││││││ no matching method found `+(::Char, ::Char)`: (x::Char + y::Char)
││││││││││││└────────────────
│││││││││┌ @ reduce.jl:49 Base.reduce_empty_iter(op, itr)
││││││││││┌ @ reduce.jl:378 Base.reduce_empty_iter(op, itr, Base.IteratorEltype(itr))
│││││││││││┌ @ reduce.jl:379 Base.reduce_empty(op, eltype(itr))
││││││││││││┌ @ reduce.jl:355 Base.reduce_empty(op.rf, T)
│││││││││││││┌ @ reduce.jl:347 Base.reduce_empty(+, T)
││││││││││││││┌ @ reduce.jl:338 zero(T)
│││││││││││││││ no matching method found `zero(::Type{Char})`: zero(T::Type{Char})
││││││││││││││└─────────────────

Cthulhu.jl#

Interactive code explorer that let’s you navigate through a nested function call-tree and apply macros like @code_*, or @which, and more. For example, one can recursively apply @code_warntype at different levels to detect the origin of a type instability. (Note though that it might take some time to master Cthulhu.)

Important macro: @descend (or directly @descend_code_warntype)

(Cthulhu isn’t a debugger! It has only “static” information.)

using Cthulhu

A = rand(10, 10)
B = rand(10, 10)

# @descend A*B # doesn't work in Jupyter -> use REPL

10×10 Matrix{Float64}:
 0.258691  0.0464967  0.263585   0.669632   …  0.125292   0.295299   0.416137
 0.170264  0.545957   0.0158409  0.13716       0.628801   0.231691   0.561139
 0.279717  0.268466   0.173288   0.0607093     0.784124   0.610417   0.587533
 0.334335  0.593489   0.383178   0.178968      0.158849   0.0148143  0.589773
 0.189268  0.0941343  0.920828   0.297028      0.29557    0.13355    0.837223
 0.230879  0.842215   0.794186   0.894374   …  0.0796169  0.865069   0.394498
 0.670888  0.809121   0.801168   0.450059      0.926456   0.370853   0.918959
 0.693241  0.975918   0.622532   0.332599      0.0759421  0.817194   0.660174
 0.507988  0.917185   0.101032   0.793746      0.0341003  0.567199   0.870177
 0.438935  0.510296   0.0892283  0.382818      0.707844   0.50728    0.291967

Summary#

  • Start with optimising serial performance, bad serial code will be bad parallel code

  • Reduce number of allocations

    • Use @btime to check the number of allocations

    • Avoid unnecessary allocations, huge no. of them is a bad sign

  • Avoid temporary allocations

    • e.g. dot syntax for broadcasting is very useful

    • Pre-allocating result arrays can save time

  • Slicing by default copies data, use @views or view(A, 1:2, 1) to get a non-copy view

  • (Lazy) generators can be much faster for certain tasks

  • Type instability is VERY bad

    • Use @code_warntype to check for type instability

    • Avoid (non-constant) globals or work only in local scope

    • Hint return types if they are Any or Union (or rewrite code to avoid this)

    • Avoid abstract types in containers

      • Use concrete types

      • Or, for more flexibility, parametric types

    • Avoid untyped containers, never use [], use Int[]/Float[]

    • Avoid changing types, e.g. x = 1; x / 2 converts int to float

    • Isolate instabilities with computational kernels

  • Access arrays in column major order

  • Make use of performance annotations if applicable:

    • @inbounds - no bounds checking

    • @simd - fused repeated operations

    • @fastmath - fused multiply add operations

  • Remember operations have different costs, e.g. * is faster than /

References#